Prefix-Sum
前綴和
前綴和是對於數列的一種預處理
經過 O(n) 初始化過後可以在 O(1) 就取得 [a, b] 的區間和
一維前綴和
要點
功能
- query:查詢某範圍的區間和
觀念
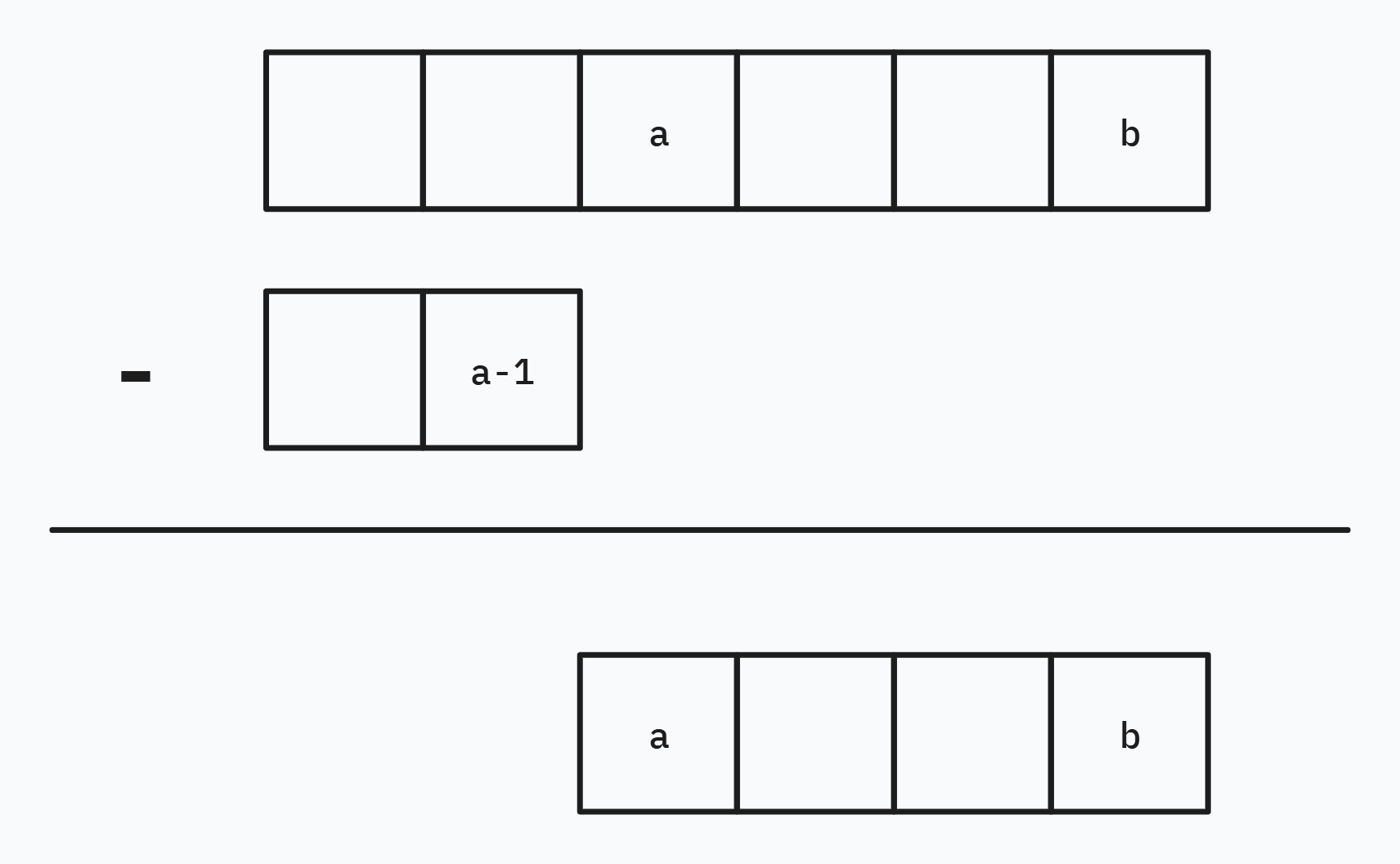
一維前綴和就是將第 N 項的數字改為 N 之前的所有總和
之後每次進行查詢我們就只需要輸出第 b 項數字減去第 a - 1 項數字
為了避免 a - 1 會減到負數
我們需要將索引改成 1-based,並將第 0 項數字設為 0
實作
陣列宣告
1
vector<int> v(n+1, 0);資料輸入
1
2
3
4
for (int i = 1; i <= n; i++) {
cin >> v[i];
v[i] += v[i-1];
}查詢
1
2
cin >> a >> b;
cout << v[b] - v[a-1];二維前綴和
要點
v[i][j] 儲存左上 ( 0, 0 ) 右下 (i, j) 內的總和
剩下的交給圖來解釋

圖片引用自 這裡
實作
宣告陣列
1
vector<vector<int>> v(row+1, vector<int>(col+1, 0));資料輸入
1
2
3
4
for (int i = 1; i <= row; i++) for (int j = 1; j <= col; j++) {
cin >> v[i][j];
v[i][j] += v[i-1][j] + v[i][j-1] - v[i-1][j-1];
}查詢
1
2
cin >> sx >> sy >> ex >> ey;
cout << v[ey][ex] - v[ey][sx-1] - v[sy-1][ex] + v[sy-1][sx-1];範例
1
2
3
4
5
6
7
8
9
10
11
12
int row, col;
cin >> row >> col;
vector<vector<int>> v(row+1, vector<int>(col+1, 0));
for(int i = 1; i <= row; i++) for (int j = 1; j <= col; j++) {
cin >> v[i][j];
v[i][j] += v[i-1][j] + v[i][j-1] - v[i-1][j-1];
}
int sx, sy, ex, ey;
cin >> sx >> sy >> ex >> ey;
cout << v[ey][ex] - v[ey][sx-1] - v[sy-1][ex] + v[sy-1][sx-1];