Maximum-Flow

中文叫做最大流，什麼是流？可以把一個圖上邊看作為水管，其權重看作為水流能夠通過的量
若圖為有向圖代表水流只允許單向流動，若為無向圖則代表可以同時往兩邊流動
而最大流是在一個圖中，在所有可能的 s-t 流（從源點 s 到 匯點 t）尋找最大值
要找到最大流可以使用 Ford-Fulkerson 演算法
但是 Ford-Fulkerson 演算法中，會因為其沒有對尋找增廣路徑的策略限制，有可能會導致不斷重複選擇非最佳解
所以我們這篇筆記主要會以 Ford-Fulkerson 的改良版：Edmonds-Karp 為主

要點

Ford-Fulkerson 觀念

s-t 流的過程會由許多大大小小的支流匯聚
演算法的目標就是不斷的尋找最適合的支流（也就是增廣路徑）並進行加總

該如何尋找增廣路徑呢？
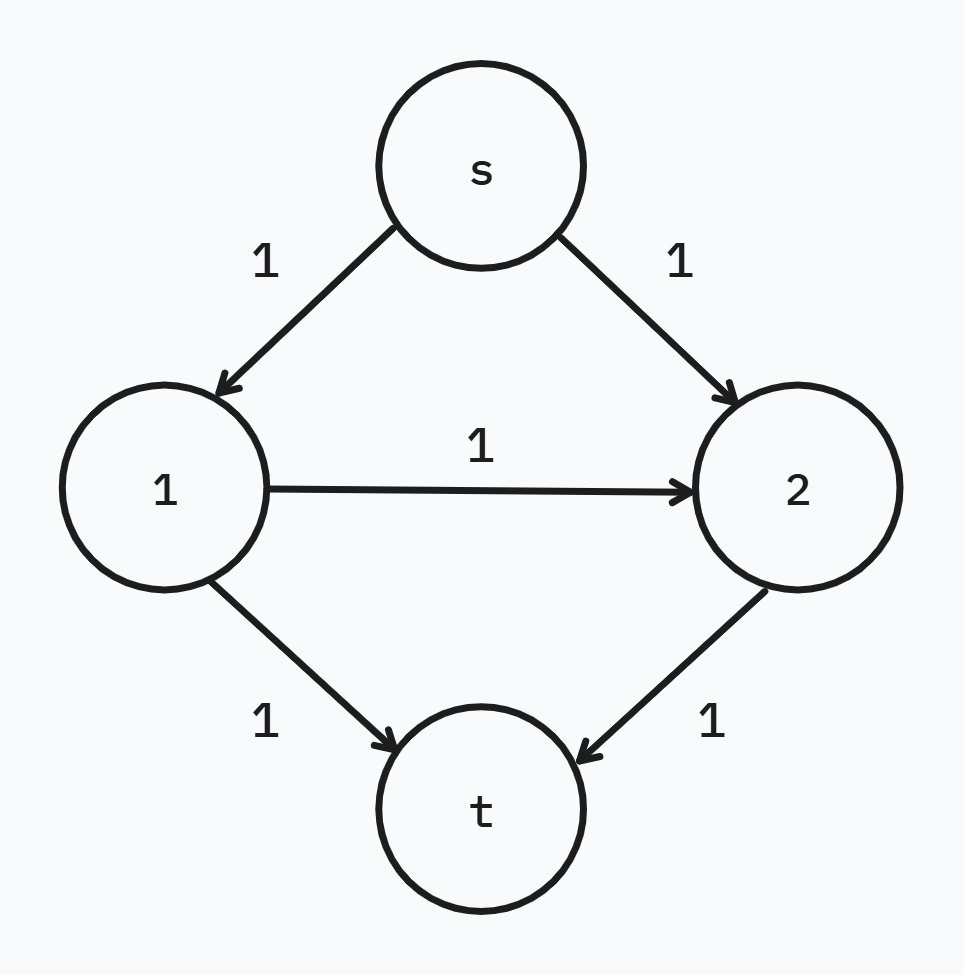
先找一條可以從 s 走到 t 的路徑
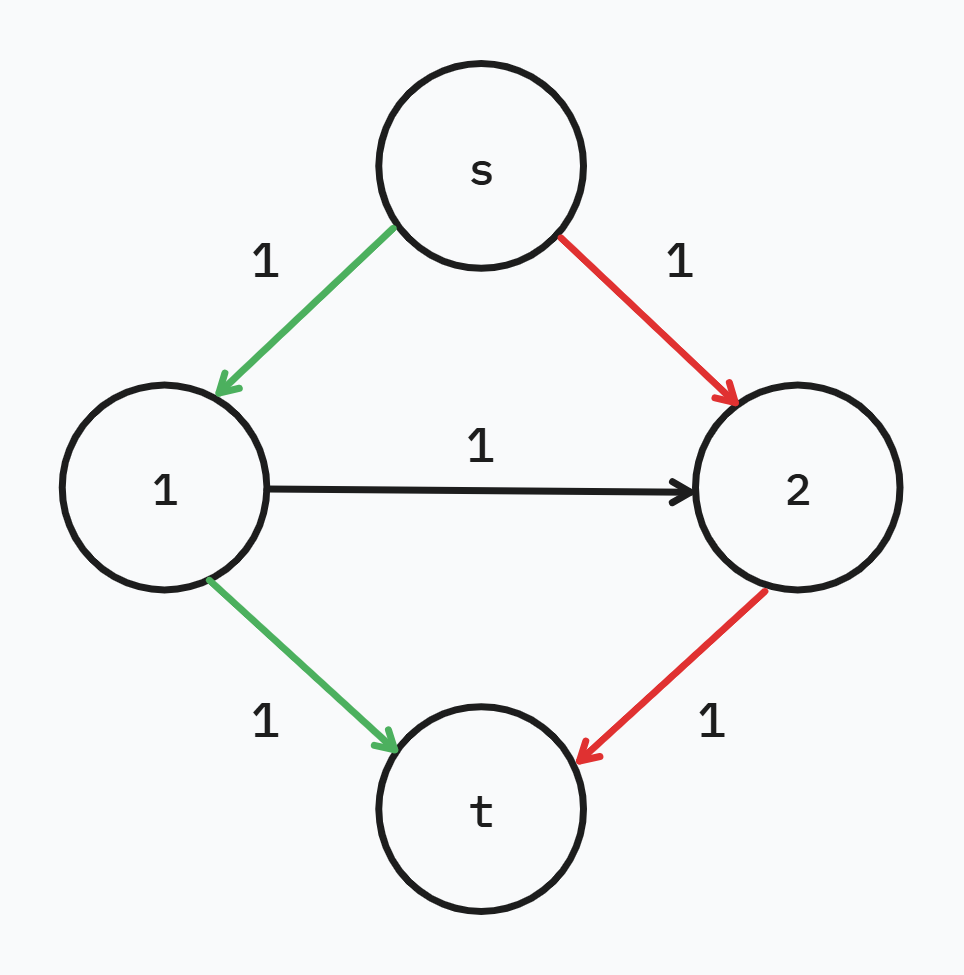
找到這條路徑中最少的水管流量
將這條路徑上的所有水管縮減該流量，如果縮減後流量為零則刪除該水管
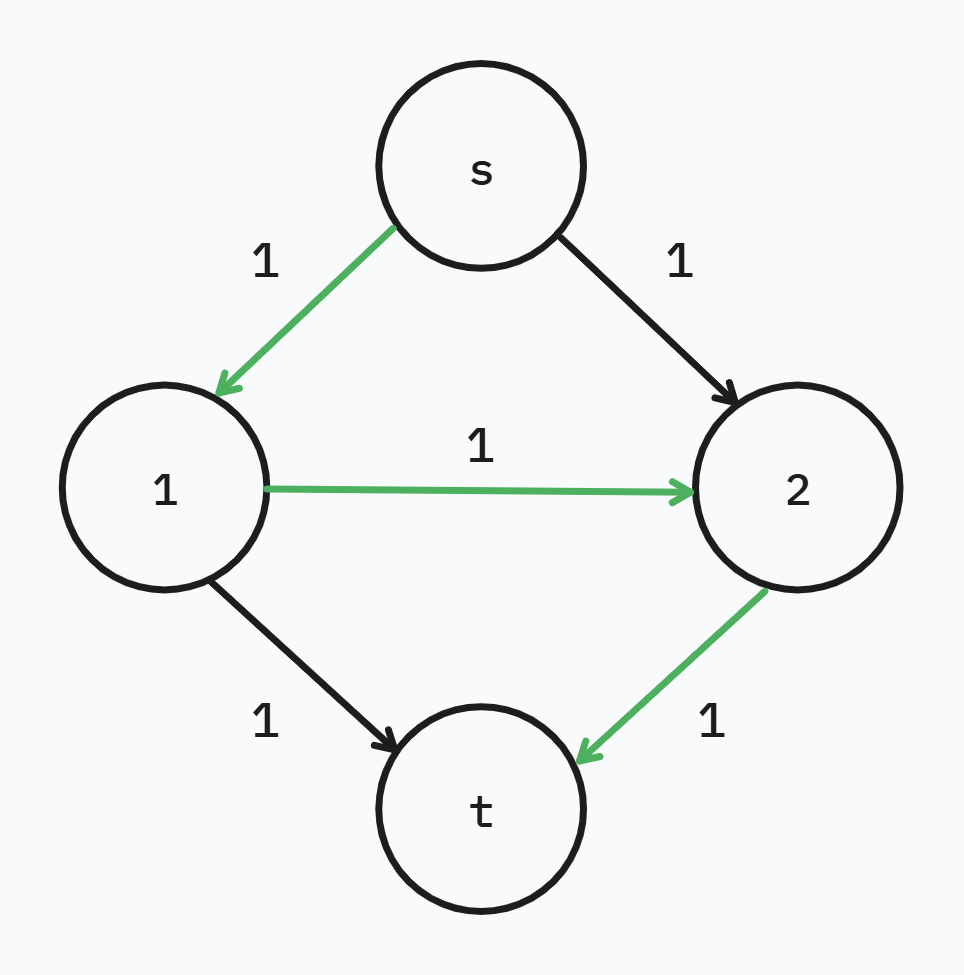
最後將該流量加到總和

但是在尋找路徑的過程中，有機會遇到找到不是最適合的路徑
因此需要有一個回溯機制
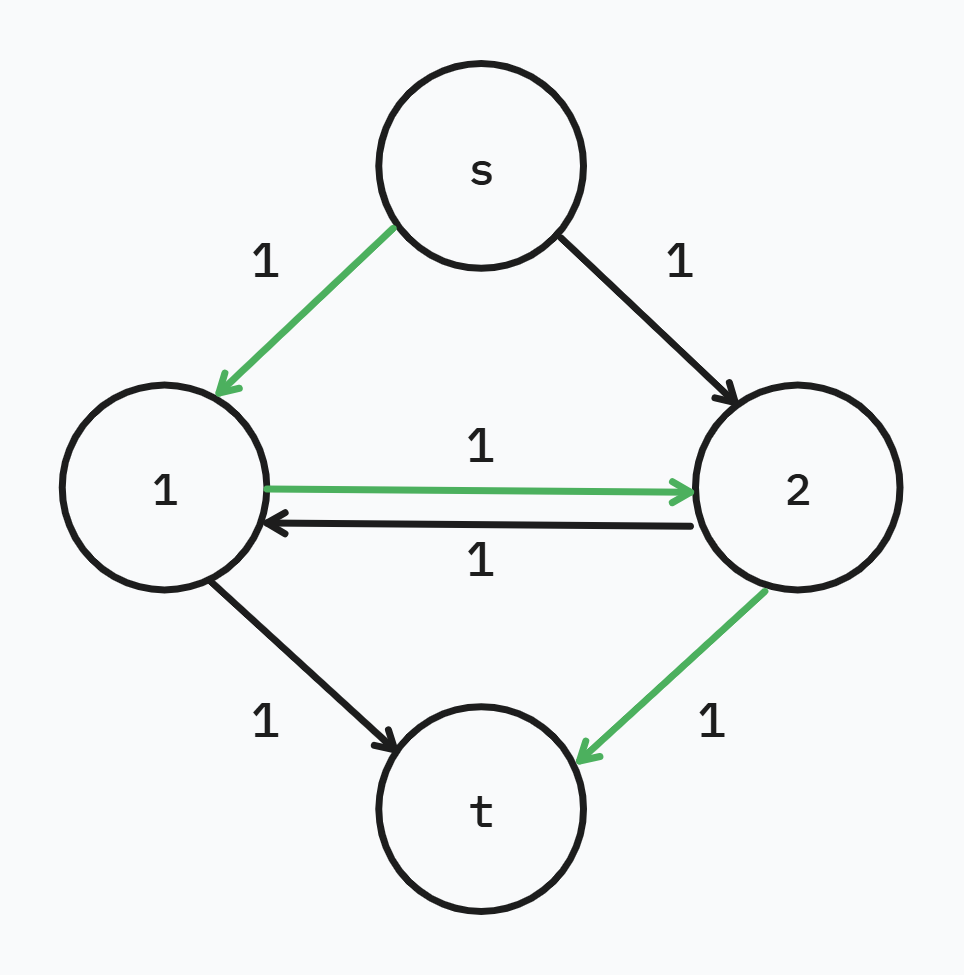
此機制可以透過建立反向流量來實現
在縮減所有水管的流量時，順便建立一條反向的同流量可以使未來的路徑連回過去的路徑
此部分透過底下的圖來解釋

原圖如下 正確的最大流路徑為下圖 最大流為 2 但因為 Ford-Fulkerson 尋找增廣路徑的方式沒有固定 有機會導致尋找到的路徑長這樣 把下一步給走死了，此時最大流只有 1 因此每找完一條路徑都要新增一條反向流量 使下一步得以繼續 透過反向流量可以成功回溯 反向流量可以使 綠前紅後、紅前綠後 組成新的路徑 最後可以找出正確的最大流 (2)

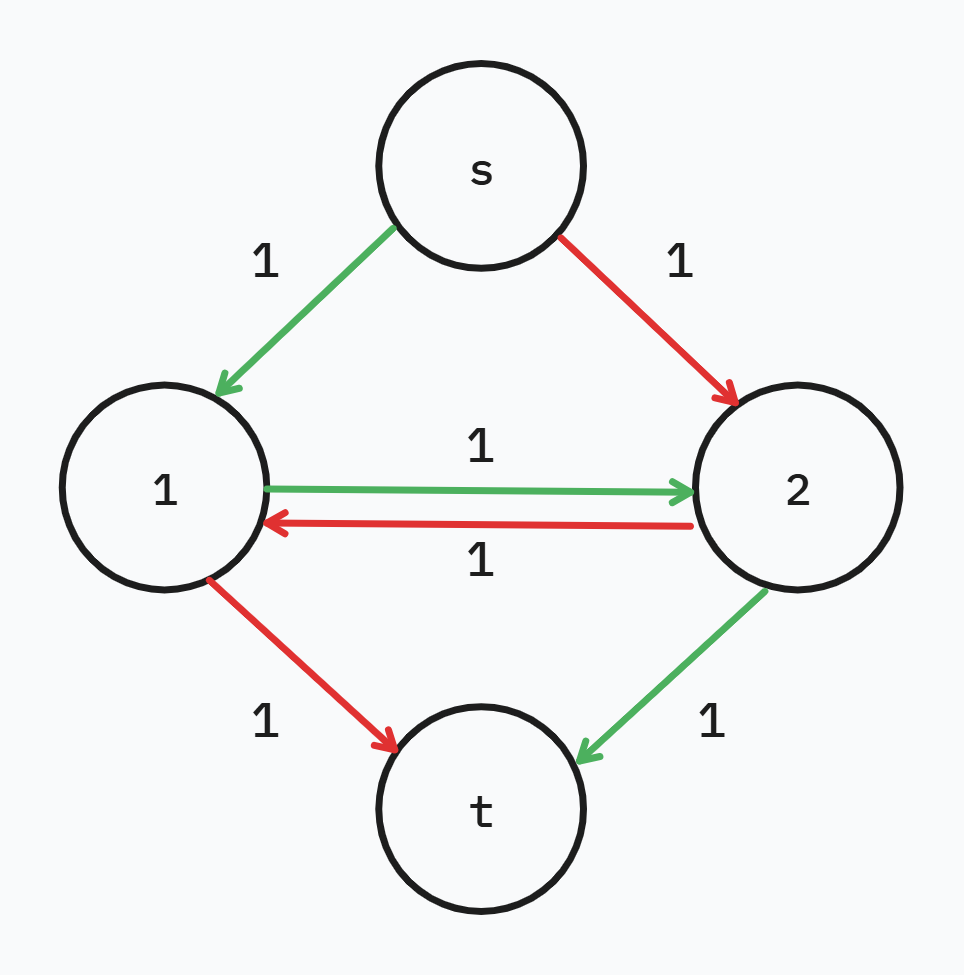
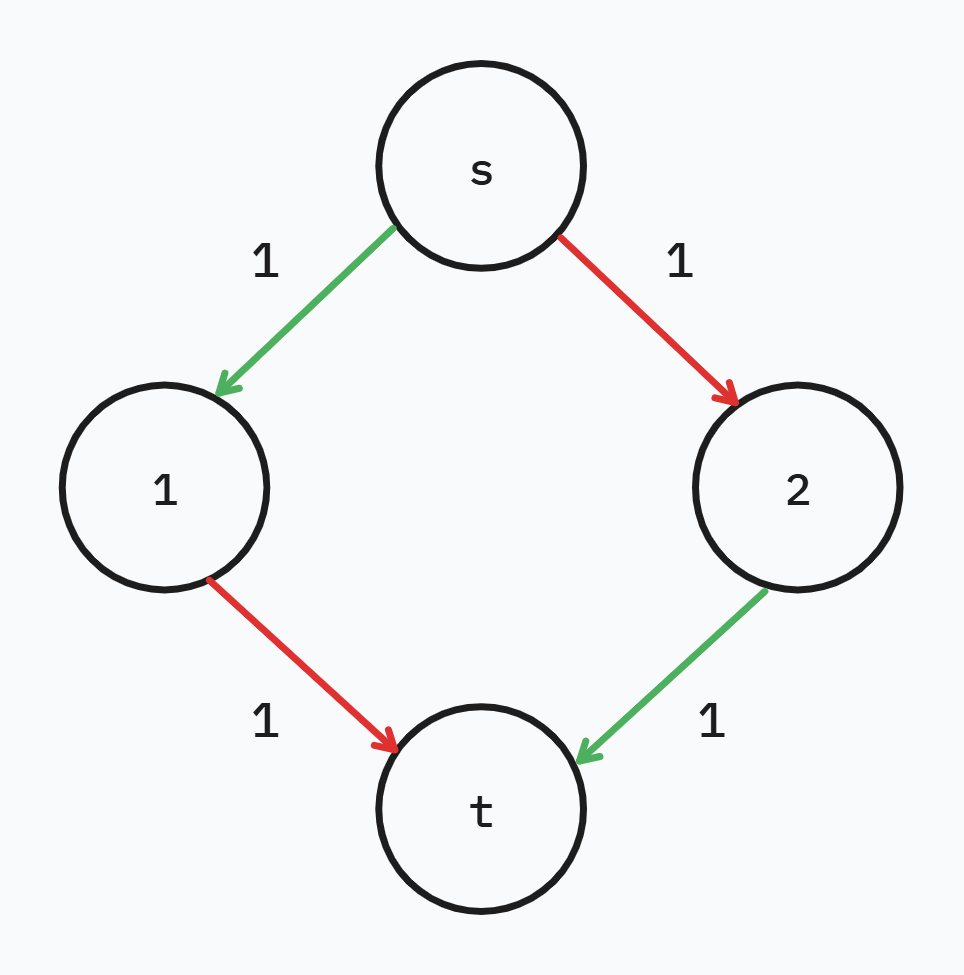
Edmonds-Karp 觀念

在 Ford-Fulkerson 中，有可能因為一直找到不合適的路徑而耗費大量時間
這時候可以透過限制每次尋找的路徑為最短路徑來解決上述問題
所以用 BFS 尋找最短路徑可以解決 Ford-Fulkerson 的缺點
這就是 Edmonds-Karp 演算法

Edmonds-Karp 要點

需要一個能夠紀錄路徑的 BFS，因此需要一維陣列紀錄拜訪過的節點在路徑中的父節點
並且需要一個二維陣列以鄰接矩陣的方式儲存圖

相較於鄰接串列，鄰接矩陣更容易還原路徑

實作

於全域宣告，使 BFS 函式可以使用

1
2
3

int n, s, e, t, a, b, w; // 節點數, 起點, 終點, 邊數, 圖, 拜訪紀錄, 路徑紀錄
vector<vector<int>> g;
vector<int> vis, par;

BFS 函式，當找到一條 s-t 路徑時，回傳 true
找不道路徑時，回傳 false

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

bool BFS() {
    queue<int> q;
    vis.assign(n+1, 0); par.assign(n+1, 0);
    q.push(s);
    while (q.size()) {
        int now = q.front(); q.pop();
        if (now == e) return true;
        for (int i = 1; i <= n; i++) if (g[now][i] && !vis[i]) { // g[now][i] 判斷兩節點之間的剩餘流量是否大於零
            vis[i] = 1;
            par[i] = now; // 紀錄路徑
            q.push(i);
        }
    }
    return false;
}

在主函式中建圖
且 g[節點][節點] 的 value 為邊的權重，也就是水管的流量

1
2
3
4
5
6

g.assign(n+1, vector<int>(n+1, 0));
cin >> s >> e >> t;
while (t--) {
    cin >> a >> b >> w;
    g[a][b] += w;
}

Edmonds-Karp 本體
如果 BFS 有找到 s-t 的路徑
就利用找到的路徑（紀錄於 par）進行計算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

int ans = 0; // 最大流計數器
while (BFS()) { // 有無找到 s-t 的路徑
    int now = e, mnF = INF; // 從終點開始，#define INF 0x3f3f3f3f
    while (now != s) { // 回推到起點
        mnF = min(mnF, g[par[now]][now]); // 尋找路徑中最小的流量
        now = par[now]; // 移動至上一個節點
    }
    now = e; // 回到終點
    while (now != s) { // 從終點回推到起點
        g[par[now]][now] -= mnF; // 縮減水管的流量
        g[now][par[now]] += mnF; // 建立反向流量
        now = par[now];
    }
    ans += mnF; // 最大流加上該流量
}
cout << "Max-Flow is " << ans; // 輸出加總，為最大流